Remember those moments in geometry class when you felt like you were navigating a maze of lines and angles? That was me, struggling with parallel and perpendicular lines. It seemed like every question presented a new challenge, a twisted path leading to a confusing solution. It wasn’t until I uncovered the hidden connections and patterns within these lines that everything clicked. This unit wasn’t just about lines and angles; it was about the fascinating world of spatial relationships, where every line held a story to tell.

Image: studylibrarydustin.z13.web.core.windows.net
In this blog post, we’ll delve into the world of parallel and perpendicular lines, a crucial concept in Geometry Unit 3. We’ll explore the fundamentals, unravel the mysteries behind these lines, and break down the complexities into clear explanations that will make sense even to those who have always considered themselves geometry-challenged. We’ll be your guide, leading you through this unit with confidence and understanding.
Parallel and Perpendicular Lines: The Foundation of Geometry
Parallel and perpendicular lines are fundamental concepts in Geometry Unit 3, forming the building blocks for understanding more complex geometric shapes and theorems. They are not simply lines on a page but a visual representation of interconnected relationships within a spatial plane.
What are Parallel Lines?
Imagine two train tracks, stretching endlessly into the horizon. Those tracks represent parallel lines, never intersecting no matter how far they extend. In geometric terms, parallel lines lie within the same plane and maintain equal distances from each other, always running alongside each other.
What are Perpendicular Lines?
Now envision the crossroads where those train tracks intersect a perpendicular road. That road signifies a perpendicular line, forming a right angle (90 degrees) with the tracks. Perpendicular lines intersect at a distinct point, creating a clear intersection and a crucial angle.
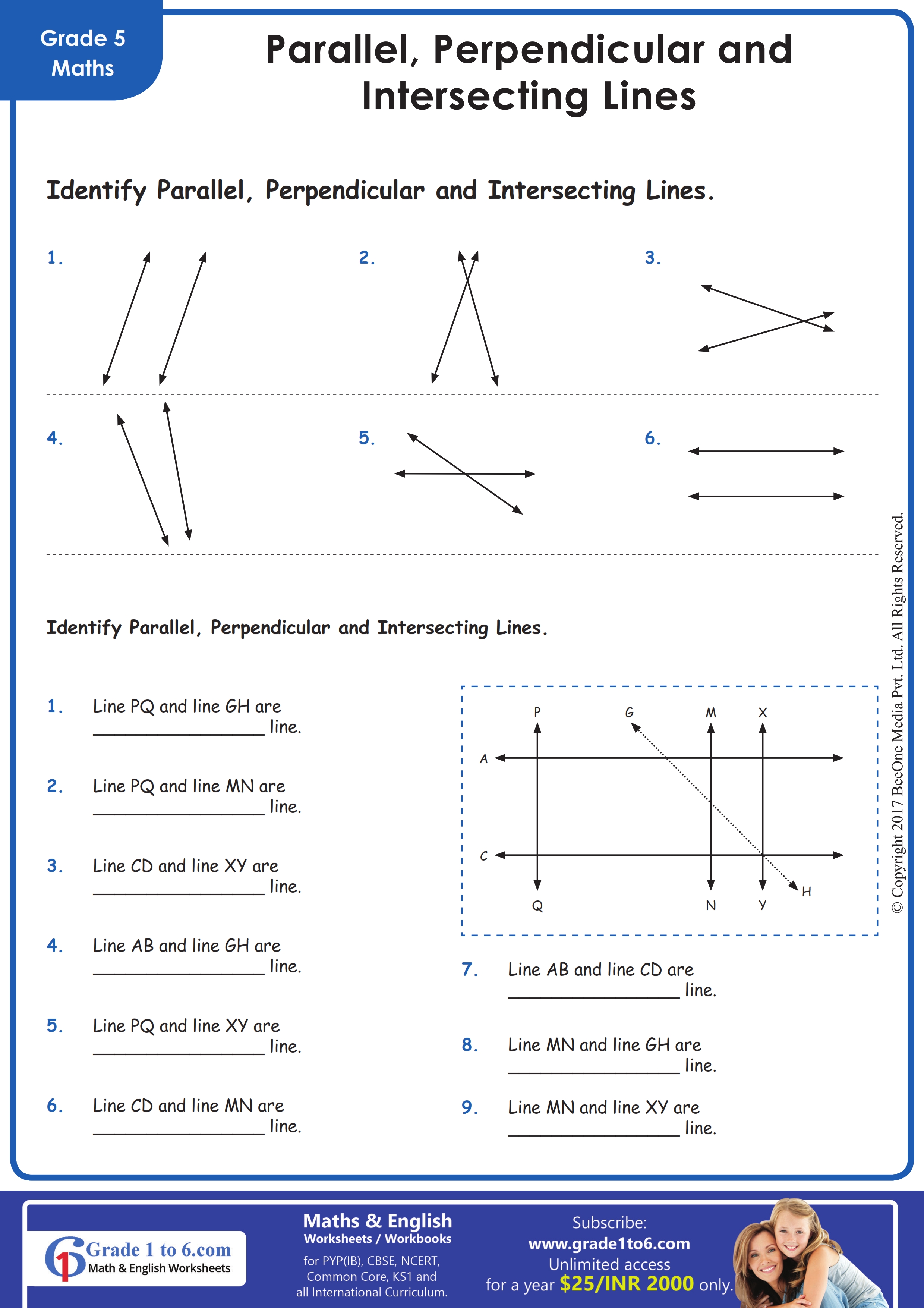
Image: www.grade1to6.com
Unlocking the Secrets of Parallel and Perpendicular Lines
Understanding the characteristics of parallel and perpendicular lines is crucial to navigating geometry effectively. Here’s a breakdown of key concepts:
Angles Formed by Parallel Lines and a Transversal
A transversal cuts across two parallel lines, creating various angles within the framework. These angles have unique relationships:
- Corresponding Angles: Located in the same relative position on each line. These angles are always congruent.
- Alternate Interior Angles: Located between the parallel lines, on opposite sides of the transversal. These angles are also always congruent.
- Alternate Exterior Angles: Located outside the parallel lines, on opposite sides of the transversal. Like alternate interior angles, these are congruent.
- Same-Side Interior Angles: Located between the parallel lines, on the same side of the transversal. These angles are supplementary, meaning they add up to 180 degrees.
Properties of Perpendicular Lines:
Perpendicular lines hold special characteristics that differentiate them from other lines in a plane:
- Right Angles: The most defining feature of perpendicular lines is that they intersect at a right angle (90 degrees).
- Slopes: The slopes of perpendicular lines are negative reciprocals of each other. If one line has a slope of m, the perpendicular line has a slope of -1/m.
- Distance: Perpendicular lines are the shortest distance between two parallel lines. They provide a precise measurement between parallel lines.
Navigating the Maze: Tips for Success
Geometry Unit 3 can seem daunting, but with a strategic approach and a few helpful tips, you’ll navigate it with confidence. Here’s how to master the intricacies of parallel and perpendicular lines:
Visualize and Sketch:
Visualizing geometric concepts is central to understanding them. Sketching diagrams helps you grasp the relationships between lines and angles, making it easier to apply theorems and identify relevant information.
Practice, Practice, Practice:
Geometry, much like any other skill, is best honed through practice. Work through various problems, focusing on different applications of parallel and perpendicular line properties. Don’t hesitate to seek help or review relevant concepts when needed.
Seek Patterns:
Recognize patterns and relationships within the concepts. Notice how angles are connected, how slopes are related, and how various theorems relate to each other. Identifying these connections will simplify the process of solving problems and deepen your understanding of the unit.
FAQs – Clarifying the Concepts
Q: What is the difference between parallel lines and perpendicular lines?
A: Parallel lines never intersect, maintaining a constant distance between them. They have the same slope. Perpendicular lines intersect at a right angle (90 degrees). Their slopes are negative reciprocals of each other.
Q: How do I determine if two lines are parallel or perpendicular?
A: You can determine parallelism by examining their slopes. If the slopes are equal, the lines are parallel. For perpendicular lines, the slopes are negative reciprocals. These relationships simplify the analysis of line orientations.
Q: What is the significance of parallel and perpendicular lines in geometry?
A: Parallel and perpendicular lines form the foundation for understanding more complex geometric shapes and theorems. They are fundamental to constructing geometric figures, analyzing triangles, and exploring spatial relationships.
Geometry Unit 3 Parallel And Perpendicular Lines Answer Key
Conclusion: Mastering the Fundamentals
Understanding parallel and perpendicular lines is like learning the alphabet of geometry. It provides the building blocks to decipher more complex geometric concepts. So, focus on mastering the fundamentals, practice, seek patterns, and don’t be afraid to ask questions.
Are you interested in exploring more advanced applications of parallel and perpendicular lines? Let us know in the comments below!






