Remember that high school algebra class where you were first introduced to the concept of the mean? You learned how to calculate the average of a set of numbers, a useful tool for analyzing data. But what about situations where the usual arithmetic mean just doesn’t cut it? Enter the geometric mean, a powerful tool that takes center stage when dealing with data that grows exponentially or undergoes multiplicative changes. I vividly recall struggling with a worksheet on the geometric mean in my own high school days. The concept initially seemed confusing, but once I grasped it, I realized its beauty and versatility. Just like me, you too can unlock the secrets of this fascinating mathematical calculation.
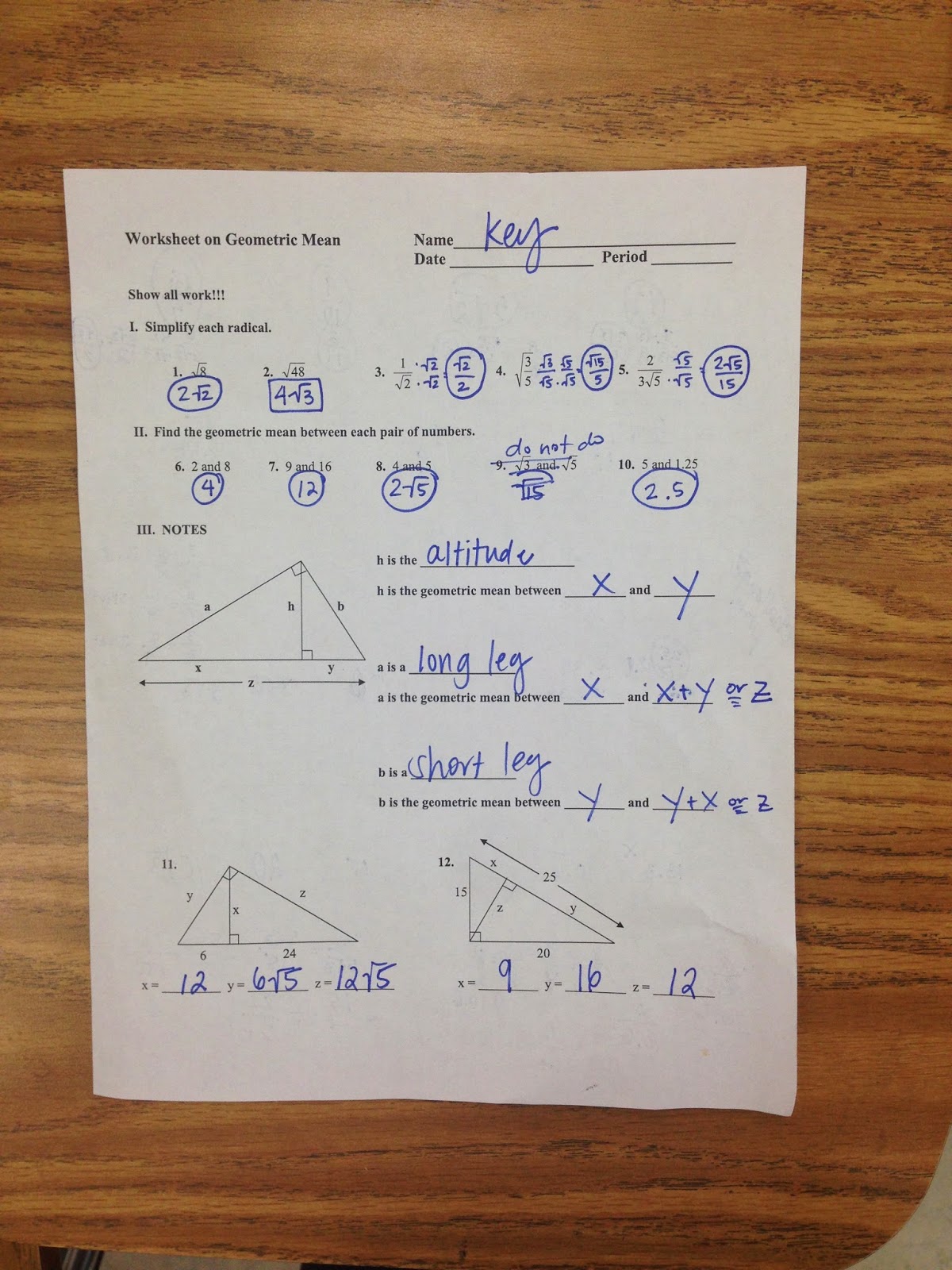
Image: gmbar.co
From calculating compound interest rates to assessing investment returns, analyzing population growth, and much more, the geometric mean is a versatile tool with widespread applications in various fields. It is particularly useful when working with data that exhibits multiplicative growth or decay. Don’t worry if you feel a little overwhelmed at first – this blog post will guide you through the process of understanding and utilizing the geometric mean. Get ready to equip yourself with the knowledge and tools to tackle Worksheet 8.1 and beyond, confidently navigating the world of data analysis using the geometric mean.
Delving into the Geometric Mean: Its Meaning and Applications
The geometric mean is a type of average that is particularly useful for data that grows exponentially or undergoes multiplicative changes. Unlike the arithmetic mean, which simply adds up all the values and divides by the number of values, the geometric mean takes the product of all values and then finds the nth root, where n is the number of values in the set. This method ensures that all values contribute equally to the final result, regardless of their magnitude.
The geometric mean is particularly relevant in situations where the data is not directly additive. Consider an investment that grows at a compound interest rate. Each year, the investment increases by a certain percentage of the previous year’s value. In this case, using the arithmetic mean to calculate the average growth rate would be misleading. Instead, the geometric mean provides a more accurate representation of the average growth over the entire investment period.
Understanding the Geometric Mean: A Step-by-Step Explanation
What is the Geometric Mean?
The geometric mean (GM) is calculated by multiplying all the values in a set together and then taking the nth root, where n is the number of values in the set. This can be represented mathematically as follows:
GM = (x1 * x2 * x3 * … * xn)1/n
Where:
- GM represents the geometric mean
- x1, x2, x3, …, xn are the values in the data set
- n is the number of values in the data set

Image: walthery.net
Why Use the Geometric Mean?
The geometric mean is crucial for situations involving multiplicative changes or growth rates, where the arithmetic mean can be misleading. Here’s why:
- Preserves Proportions: The geometric mean considers the relative changes between values, ensuring a more accurate representation of average growth, especially in cases where growth is exponential.
- Handles Negative Values: Unlike the arithmetic mean, the geometric mean can be calculated even when the data set includes negative values.
- Applicable to Ratios: If working with ratios or percentages, the geometric mean provides a better measure compared to the arithmetic mean because it accounts for the multiplicative relationships between the values.
Calculating the Geometric Mean: A Practical Example
Let’s illustrate this with an example. Consider an investment that grew by 10% in the first year, 15% in the second year, and 20% in the third year. To find the average growth rate using the geometric mean, we follow these steps:
- Convert percentages to growth factors: 10% = 1.10, 15% = 1.15, and 20% = 1.20
- Multiply the growth factors together: 1.10 * 1.15 * 1.20 = 1.518
- Take the cube root (since there are three years): 1.5181/3 = 1.147
- Convert the result back to a percentage: 1.147 – 1 = 0.147 = 14.7%
Therefore, the geometric mean growth rate of the investment is 14.7%, providing a more accurate representation of the overall growth compared to simply averaging the individual growth percentages.
Trends and Developments in Geometric Mean Applications
The geometric mean continues to be an essential tool in various fields, and its applications are expanding with the increasing complexity of data analysis. Here are some key trends and developments:
- Financial Analysis: The use of the geometric mean in financial modeling and investment analysis is growing, particularly for calculating portfolio returns and analyzing the performance of assets over time.
- Medical Research: The geometric mean is widely used in medical research for calculating average changes in biological variables and interpreting outcomes in clinical trials.
- Environmental Studies: Environmental scientists use the geometric mean to analyze data related to air and water pollution levels, tracking longitudinal changes in environmental variables over time.
The accessibility of data and the rise of sophisticated analytical tools are contributing to the broader adoption of the geometric mean in various fields. Researchers and analysts are increasingly realizing the importance of this powerful tool for uncovering meaningful insights from data that exhibits complex patterns.
Unlocking the Power of the Geometric Mean: Tips and Expert Advice
Tip 1: Know When to Use the Geometric Mean
The geometric mean is not a one-size-fits-all solution. Its application is most appropriate for scenarios involving multiplicative growth or changes, where data values are interconnected through multiplication. A clear understanding of the data and the underlying processes will help you determine whether the geometric mean is the appropriate tool to use.
Tip 2: Understand the Implications of Using the Geometric Mean
When interpreting the results of geometric mean calculations, it’s crucial to consider the context. Keep in mind that the geometric mean represents an average growth rate, not necessarily the individual growth rates of each data point. Being aware of the potential limitations and interpretations is vital for drawing meaningful conclusions from your analysis.
Frequently Asked Questions (FAQs)
Q: What are some real-world examples of the geometric mean in action?
A: The geometric mean is used in a wide range of disciplines. Here are some real-world examples:
- **Investing:** To calculate the average annual return on an investment over multiple years, particularly when dealing with compounding interest.
- **Population Growth:** To determine the average annual growth rate of a population over a specific period.
- **Medical Research:** To analyze the average change in a specific biological indicator, such as blood pressure or cholesterol levels, over time in a clinical trial.
- **Environmental Monitoring:** To calculate the average concentration of pollutants over a series of measurements taken at different time points.
Q: Why is the geometric mean used instead of the arithmetic mean in some situations?
A: The arithmetic mean can be misleading when dealing with data that undergoes multiplicative growth or changes. The geometric mean provides a more accurate representation of the average growth rate by taking into account the multiplicative relationships between data points.
Q: How do I calculate the geometric mean using a calculator or spreadsheet software?
A: Most calculators and spreadsheet software like Microsoft Excel have built-in functions for calculating the geometric mean. Look for a function labeled “GEOMEAN,” “GM,” or a similar variation in the statistical or mathematical functions. You can also use the formula mentioned earlier to calculate it manually.
Worksheet 8.1 Geometric Mean Answer Key
Conclusion
The geometric mean is a powerful tool for analyzing data that grows exponentially or undergoes multiplicative changes. It provides a more accurate and meaningful representation of average growth compared to the usual arithmetic mean. By understanding the concepts and applications of the geometric mean, you can unlock valuable insights from your data, making informed decisions in various fields, from finance to healthcare and beyond.
Are you interested in learning more about the geometric mean and its applications in your field of interest? Let me know in the comments below!






