Have you ever wondered what lies behind the veil of the AP Calculus BC Multiple Choice questions? These notoriously challenging exams test the limits of your calculus knowledge, leaving many students feeling both excited and apprehensive. While the actual 2019 AP Calculus BC MCQs are closely guarded, we can delve into the patterns and concepts tested in those questions, understanding what made them unique and how to approach them effectively.

Image: studentlanka.com
This exploration isn’t just about cracking the code of a past exam. It’s about acquiring a deeper understanding of the fundamental concepts covered in Calculus BC and recognizing the ways in which the College Board assesses your mastery. By analyzing the trends from the 2019 exam, we can glean valuable insights and equip ourselves with the tools needed to tackle future AP Calculus challenges.
Exam Structure and Content: A Glimpse into the 2019 AP Calculus BC MCQ Landscape
The 2019 AP Calculus BC Multiple Choice section, as with any other year, consisted of 45 questions. Each correct answer was worth 1 point, resulting in a maximum score of 45 points for this part of the exam. Time management was crucial, as students had 1 hour and 30 minutes to complete the entire multiple choice section.
The questions were categorized into two main groups:
- Calculator-Allowed (28 questions): These questions required the use of a graphing calculator to solve them effectively. The calculator wasn’t a magic wand that solved everything; it was a tool to help visualize functions, compute values, and explore complex graphical relationships.
- No-Calculator (17 questions): These questions relied heavily on your knowledge of calculus concepts, formulas, and techniques. You couldn’t depend on a graphing calculator for assistance, instead relying on analytical problem-solving and conceptual understanding.
The Key Players: Topics Covered in the 2019 AP Calculus BC Multiple Choice
The AP Calculus BC exam focuses on a broad range of topics, spanning from differential calculus to integral calculus and venturing into the fascinating world of sequences and series. The 2019 MCQ covered the following key areas:
1. Limits and Continuity
Limits and continuity formed the foundation of calculus, and the 2019 exam reflected this importance. Questions tested your ability to find limits using various techniques, analyze the continuity of functions, and understand the relationship between limits and continuity.
Here’s an example of a common type of question:**
Example: Given the function f(x) = (x^2 – 4)/(x – 2) for x ≠ 2 and f(2) = 3, determine the value of lim_(x→2) f(x).
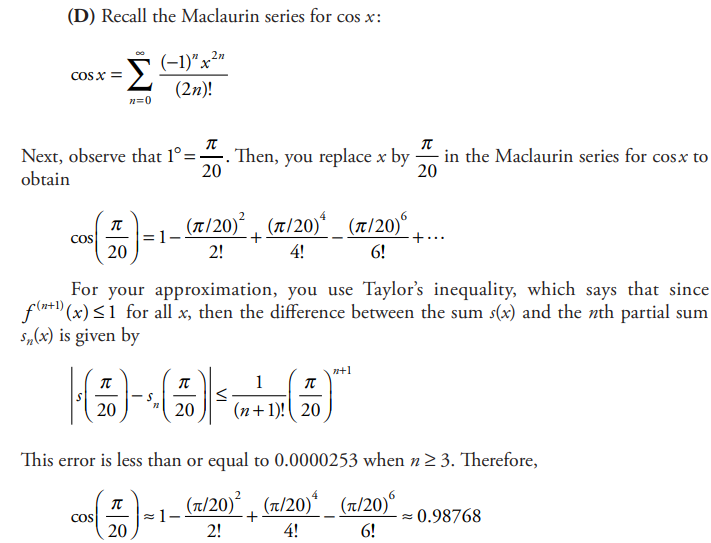
Image: www.iitianacademy.com
2. Derivatives
Derivatives are at the heart of differential calculus, measuring rates of change and providing insights into the behavior of functions. The 2019 AP Calculus BC MCQ covered a wide range of derivative concepts:
- Basic Differentiation: Calculating derivatives using rules like the power rule, product rule, quotient rule, and chain rule.
- Implicit Differentiation: Finding derivatives of functions defined implicitly, where one variable is not explicitly expressed in terms of the other.
- Related Rates: Solving problems involving rates of change of variables that are related to each other.
- Applications of Derivatives: Using derivatives to find critical points, intervals of increasing or decreasing functions, points of inflection, and maximum or minimum values.
Example: Find the equation of the tangent line to the curve defined by the equation x^2 + y^2 = 25 at the point (3, 4).
3. Integrals
Integrals are the inverse operation of derivatives, allowing us to calculate areas, volumes, and other quantities. The 2019 AP Calculus BC MCQ explored a variety of integration methods:
- Indefinite Integrals: Finding the antiderivative of a function.
- Definite Integrals: Calculating the definite integral of a function over a given interval, representing the area under the curve.
- Integration Techniques: Mastering techniques like integration by substitution, integration by parts, and trigonometric integration.
- Applications of Integrals: Solving problems involving area, volume, arc length, and work.
Example: Calculate the definite integral: ∫(0 to π/2) sin(x) dx
4. Differential Equations
Differential equations form a bridge between calculus and the real world, modeling phenomena like population growth, radioactive decay, and motion. The 2019 AP Calculus BC MCQ explored various aspects of differential equations:
- Solving Differential Equations: Using techniques like separation of variables, integrating factors, and homogeneous equations to find solutions.
- Applications of Differential Equations: Modeling real-world scenarios, interpreting solutions, and understanding their implications.
Example: Solve the differential equation: dy/dx = xy with the initial condition y(0) = 1.
5. Sequences and Series
Sequences and series explore the concept of sums of an infinite number of terms, opening up a world of fascinating mathematical possibilities. The 2019 AP Calculus BC MCQ included questions related to:
- Sequences: Understanding patterns, finding limits, and classifying sequences.
- Series: Determining convergence or divergence, finding sums of convergent series, and applying techniques like the ratio test, integral test, and comparison test.
- Power Series: Representing functions as power series, finding intervals of convergence, and using Taylor or Maclaurin series.
Example: Determine whether the series ∑(n=1 to ∞) 1/n^2 converges or diverges, and if it converges, find its sum.
Navigating the 2019 AP Calculus BC MCQ Challenge: Tips and Strategies
The 2019 AP Calculus BC MCQ wasn’t just about rote memorization. It demanded a deep understanding of concepts, the ability to apply those concepts to various situations, and the skills to navigate through challenging problems systematically. Here are some tips and strategies to navigate the challenges of a similar AP Calculus BC MCQ:
1. Mastering the Fundamentals
The foundation of success in any calculus exam lies in a solid grasp of the fundamentals. This means understanding the definitions, theorems, and formulas related to limits, derivatives, integrals, and sequences and series.
2. Practice, Practice, Practice
Practice is key to success in any subject, but it’s especially crucial for AP Calculus. Work through as many practice problems as you can, from textbooks, online resources, and past exams. This will help you solidify your understanding and build confidence in tackling various question types.
3. Time Management
Time is of the essence. Knowing how much time to allocate to each question is important. Don’t get bogged down in a single problem for too long. If you’re stuck, move on and come back to it later.
4. Process of Elimination
When faced with a challenging question, the process of elimination can be a valuable strategy. eliminate incorrect answer choices to narrow down your options and increase your chances of selecting the correct answer.
5. Using Your Calculator Wisely
For the calculator-allowed questions, use your graphing calculator to your advantage. Visualize functions, find critical points, calculate integrals, and explore graphical relationships. But remember, your calculator is a tool, not a magic solution. Understanding the underlying concepts is still crucial.
6. Seeking Help When Needed
Don’t hesitate to seek help if you’re struggling with a concept. Ask your teacher, classmates, or consult online resources. There’s no shame in seeking support; it’s a sign of proactive learning and a commitment to success.
2019 Ap Calc Bc Mcq Answers
Beyond the 2019 AP Calculus BC MCQ: A Look Ahead
The 2019 AP Calculus BC MCQ was a snapshot in time, but the fundamental concepts and strategies it tested remain relevant. By understanding the patterns and trends, we can prepare ourselves for future exams, appreciating the beauty and power of calculus in its full complexity.
The AP Calculus BC exam is an exciting and challenging journey. It’s a chance to stretch your intellectual muscles, unravel the intricate workings of calculus, and equip yourself with skills that will open doors to fascinating career paths and academic pursuits. So, whether you’re a current student facing the upcoming exam or a curious explorer delving into the world of calculus, remember that the key to success lies in a combination of hard work, strategic thinking, and a passion for understanding.






