Remember that agonizing math assignment in high school? The one with those pesky linear functions? I remember feeling so lost, trying to decipher the slopes, intercepts, and equations. It was like a foreign language! But thanks to a well-designed practice worksheet, everything finally clicked. It wasn’t just about filling in blanks; it was about understanding the core principles of linear functions and how they relate to the real world. It was a game-changer. And that’s the power of a quality practice worksheet – it demystifies complex concepts and turns them into manageable chunks of knowledge.
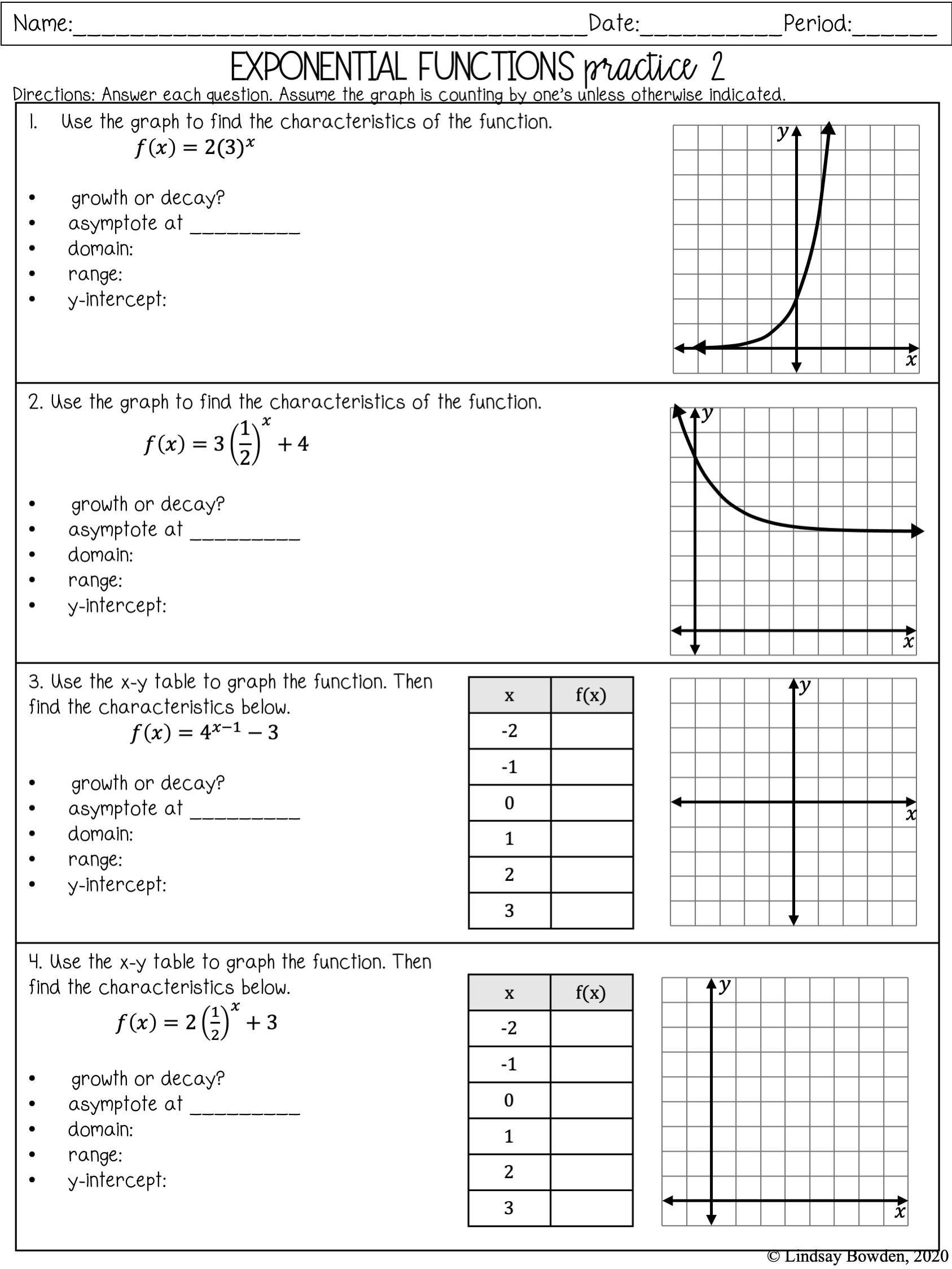
Image: lindsaybowden.com
Today, we’ll delve into the fascinating world of “Characteristics of Linear Functions Practice Worksheet A”. This worksheet is a gateway to mastering linear functions, paving the way for a deeper understanding of algebra and its applications in various fields. We’ll break down the key concepts, explore practical examples, and provide you with essential tips to navigate this crucial learning journey.
Understanding the Essence of Linear Functions
What are Linear Functions?
At its core, a linear function represents a straight line on a graph. It’s a relationship between two variables (usually denoted as *x* and *y*) where for every change in *x*, there’s a corresponding consistent change in *y*. This consistency makes linear functions predictable and easy to analyze. Picture a car driving at a constant speed – its distance traveled over time forms a linear function: a steady increase in distance for each unit of time.
Key Characteristics & Components
Linear functions are characterized by two primary components:
- Slope: The slope measures the steepness or inclination of the line. It indicates how much *y* changes for every unit change in *x*. A positive slope means the line rises from left to right, while a negative slope indicates a downward trend.
- Y-intercept: This is the point where the line crosses the vertical (y) axis. It represents the value of *y* when *x* is zero. The y-intercept is often denoted as the constant term (b) in the linear function equation (y = mx + b).
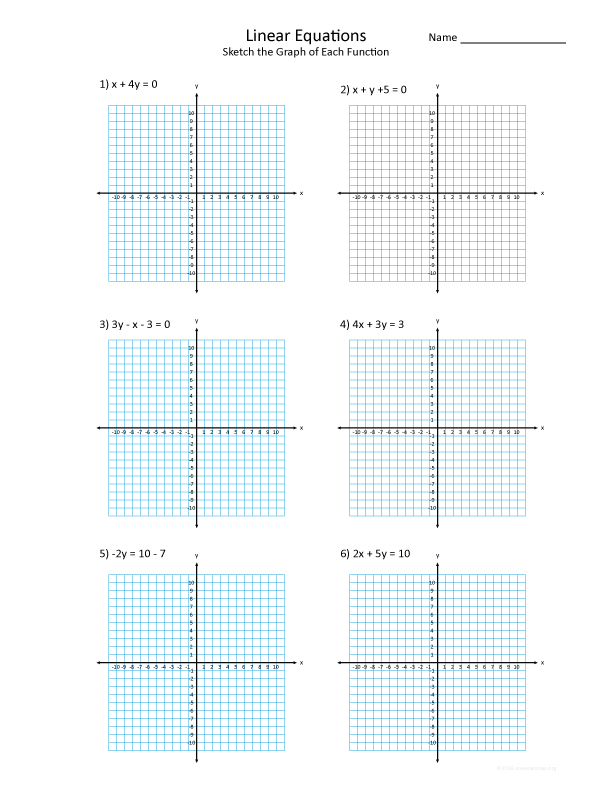
Image: www.functionworksheets.com
Types of Linear Equations
Linear functions can be expressed in various forms, each revealing different insights about the relationship between the variables:
- Slope-intercept form (y = mx + b): This is the most common form, making the slope (m) and y-intercept (b) immediately apparent.
- Point-slope form (y – y1 = m(x – x1)): This form uses a specific point (x1, y1) on the line and the slope (m) to define the equation.
- Standard form (Ax + By = C): This form is useful for understanding the relationship between the coefficients (A, B, C) and the line’s properties.
Navigating the “Characteristics of Linear Functions Practice Worksheet A”
Practice Worksheet A is designed to solidify your understanding of linear functions’ key characteristics. It typically presents a set of linear equations and asks you to identify their slope, y-intercept, and other attributes. Here’s a breakdown of common exercises:
Exercise 1: Identifying Slope and Y-intercept
The most basic exercise involves looking at a linear equation in slope-intercept form (y = mx + b) and simply extracting the slope (m) and y-intercept (b). For example, in the equation y = 2x + 3, the slope is 2, and the y-intercept is 3. These elements provide immediate insights into the line’s behavior.
Exercise 2: Graphing Linear Functions
This exercise focuses on visualizing the linear function. You’ll be given an equation and asked to plot it on a coordinate plane. To graph, you can utilize the slope and y-intercept. Start by plotting the y-intercept on the y-axis. Then, using the slope, move up or down (depending on whether it’s positive or negative) and to the right one unit (or vice versa). Connect the points to draw the line.
Exercise 3: Writing Linear Equations
Here, you’ll be given information about a linear function, such as two points or the slope and one point. You’ll need to use this information to write the equation of the line. For example, if you know the slope is 3 and the line passes through the point (1, 2), you can use the point-slope form (y – y1 = m(x – x1)) to derive the equation.
Exercise 4: Solving Systems of Linear Equations
This exercise involves working with two or more linear equations simultaneously. You need to find the solution where the lines intersect. Several methods can be used to solve systems, including substitution, elimination, or graphing. Each method offers a unique approach to finding the common point that satisfies all the equations.
Mastering the Fundamentals: Tips and Expert Advice
Navigating practice worksheets requires a strategic approach. Here are some crucial tips based on my own experiences:
- Understand the Basics: Ensure you have a solid grasp of the foundational concepts like slope, y-intercept, and different equation forms before attempting the worksheet.
- Review Examples: Scrutinize solved examples from your textbook or online resources to see how problems are approached and solved. This allows you to learn by observing and imitating.
- Practice Consistently: The key to mastery is consistent practice. Don’t hesitate to revisit problem types you find challenging until you feel confident. Repetition reinforces the learning process.
- Visualize and Interpret: Often, understanding a concept is easier when you visualize it. Make use of graphing tools and draw diagrams to better comprehend the relationship between equations and their graphical representations.
- Seek Help When Needed: Don’t be afraid to ask your teacher, a tutor, or classmates for help when you encounter difficulties. Collaborative learning can often unlock the puzzle.
Remember, understanding linear functions is not just about solving problems; it’s about developing analytical skills. By breaking down complex concepts into simpler parts, you’ll gain a deeper understanding of how linear functions shape our world, from financial models to scientific research.
Frequently Asked Questions
Q: What is the significance of the slope in a linear function?
A: The slope tells you the rate of change between the two variables. It reveals the steepness of the line and how much the dependent variable (y) changes for every unit change in the independent variable (x).
Q: How does the y-intercept impact the graph of a linear function?
A: The y-intercept determines the point where the line crosses the y-axis. It is the starting point of the line and indicates the value of y when x is zero.
Q: What are some real-world examples of linear functions?
A: Linear functions are pervasive in our daily lives. Some examples include the relationship between distance and time when traveling at a constant speed, the cost of buying a certain number of items at a fixed price, or the relationship between the number of hours worked and earnings.
Q: What are some common mistakes to avoid when working with linear functions?
A: Common mistakes include misinterpreting the slope (neglecting the sign or confusing it with the y-intercept), incorrectly applying the formula, or making errors when solving systems of equations.
Q: How can I improve my understanding of linear functions further?
A: To further your understanding, explore real-world applications of linear functions in various fields. Also, consider working on additional practice problems, researching online resources, and participating in online forums for guidance and discussions.
Characteristics Of Linear Functions Practice Worksheet A
Conclusion
Mastering the “Characteristics of Linear Functions Practice Worksheet A” is a crucial step in your journey of understanding linear functions. By grasping the fundamental concepts, practicing consistently, and utilizing the tips we’ve provided, you can unlock the world of linear relationships and gain valuable insights into this essential mathematical concept. It’s not just about solving equations; it’s about developing critical thinking skills that have applications in various aspects of your life.
Are you ready to embark on this learning adventure? What are your thoughts and experiences with linear functions?






